El tiempo de concentración de una cuenca, se define como el tiempo mínimo necesario para que todos los puntos de una cuenca estén aportando agua de escorrentía de forma simultánea al punto de salida, punto de desagüe o punto de cierre. Está determinado por el tiempo que tarda en llegar a la salida de la cuenca el agua que procede del punto hidrológicamente más alejado, y representa el momento a partir del cual el caudal de escorrentía es constante.
El tiempo de concentración de la cuencaes muy importante porque en los modelos lluvia-escorrentía, la duración de la lluvia se asume igual al tiempo de concentración de la cuenca, puesto que es para esta duración cuando la totalidad de la cuenca está aportando al proceso de escorrentía, por lo cual se espera que se presenten los caudales máximos. Las diversas metodologías existentes para determinar el tiempo de concentración de una cuenca a partir de sus parámetros morfométricos, fueron determinadas a partir de ajustes empíricos de registros hidrológicos.
En la literatura existen múltiples expresiones para el cálculo del tiempo de concentración propuestas por diferentes autores: Temez, William, Kirpich, California Coulverts Practice, Giandotti, S.C.S, Ventura -Heron, Brausby-William, Passini, Izzard (1946), Federal Aviation Administration (1970), Ecuaciones de onda cinemática Morgali y Linsley (1965) Aron y Erborge (1973).
Debido a las diferentes formas como fueron concebidas estas expresiones, la variabilidad de los resultados entre una y otra puede ser bastante alta, razón por la cual el criterio del analista juega un papel fundamental en la definición del tiempo de concentración de una determinada cuenca.
Témez.
Tc: Tiempo de concentración en horas, L: Longitud del cauce principal en kilómetros, So: Diferencia de cotas sobre L en porcentaje.

Williams.
A: área de la cuenca en millas cuadradas, L: distancia en línea recta desde el sitio de interés al punto mas alto en millas, So: diferencia de cotas entre los puntos más extremos divida por L en porcentaje, d: diámetro de una cuenca circular con área A en millas.
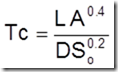
Kirpich. Desarrollada a partir de información del SCS en siete cuencas rurales de Tennessee con canales bien definidos y pendientes empinadas (3 a 10%).
L: longitud desde la estación de aforo hasta la divisoria siguiendo en cauce principal en kilómetros, So: diferencia de cotas entre los puntos extremos de la corriente en m/m.
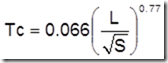
California Culverts Practice. Esencialmente es la ecuación de Kirpich; desarrollada para pequeñas cuencas montañosas en California.
L = longitud del curso de agua más largo (m), H = diferencia de nivel entre la divisoria de aguas y la salida (m).

Giandotti
tc= tiempo de concentración (horas), S= área de la cuenca (km2), L= longitud del cauce principal (km), i= elevación media de la cuenca o diferencia de nivel principal (m).

Ecuación de retardo SCS (1973).Ecuación desarrollada por el SCS a partir de información de cuencas de uso agrícola; ha sido adaptada a pequeñas cuencas urbanas con áreas inferiores a 800 Ha; se ha encontrado que generalmente es buena cuando el área se encuentra completamente pavimentada; para áreas mixtas tiene tendencia a la sobreestimación; se aplican factores de ajuste para corregir efectos de mejoras en canales e impermeabilización de superficies; la ecuación supone que tc = 1.67 x retardo de la cuenca.
L = longitud hidráulica de la cuenca mayor trayectoria de flujo (m), CN = Número de curva SCS, S = pendiente promedio de la cuenca (m/m).

Ventura-Heras
tc= tiempo de concentración (horas), i= pendiente media del cauce principal (%), S= área de la cuenca (km2), L= longitud del cauce principal (km), a= alejamiento medio

Bransby-Williams
T= tiempo de concentración (horas), L= distancia máxima a la salida (km), D= diámetro del círculo de área equivalente a la superficie de la cuenca (km2), M= área de la cuenca (km2), F= pendiente media del cauce principal (%)

Passini
tc= tiempo de concentración (horas), i= pendiente media del cauce principal (%), S= área de la cuenca (km2), L= longitud del cauce principal (km), a= alejamiento medio

Izzard
Desarrollada experimentalmente en laboratorio por el Bureau of Public Roads para flujo superficial en caminos y Áreas de céspedes; los valores del coeficiente de retardo varían desde 0.0070 para pavimentos muy lisos hasta 0.012 para pavimentos de concreto y 0.06 para superficies densamente cubiertas de pasto; la solución requiere de procesos iterativos; el producto de i por L debe ser ≤ 3800.
i = intensidad de lluvia (mm/h), c = coeficiente de retardo, L = longitud de la trayectoria de flujo (m), S = pendiente de la trayectoria de flujo (m/m).

Federal Aviation Administration
Desarrollada de información sobre el drenaje de aeropuertos recopilada por el Corps of Engineers: el método tiene como finalidad el ser usado en problemas de drenaje de aeropuertos pero ha sido frecuentemente usado para flujo superficial en cuencas urbanas.
C = coeficiente de escorrentía del método racional, L = longitud del flujo superficial (m), S = pendiente de la superficie (m/m)

Ecuaciones de onda cinemática Morgali y Linsley (1965) Aron y Erborge (1973)
Ecuación para flujo superficial desarrollada a partir de análisis de onda cinemática de la escorrentía superficial desde superficies desarrolladas; el método requiere iteraciones debido a que tanto I (Intensidad de lluvia) como Tc son desconocidos, la superposición de una curva de intensidad – duración – frecuencia da una solución gráfica directa para Tc
L = longitud del flujo superficial (m), n = coeficiente de rugosidad de Manning, I = intensidad de lluvia, mm/h, S = pendiente promedio del terreno (m/m).

El tiempo de concentración de la cuencaes muy importante porque en los modelos lluvia-escorrentía, la duración de la lluvia se asume igual al tiempo de concentración de la cuenca, puesto que es para esta duración cuando la totalidad de la cuenca está aportando al proceso de escorrentía, por lo cual se espera que se presenten los caudales máximos. Las diversas metodologías existentes para determinar el tiempo de concentración de una cuenca a partir de sus parámetros morfométricos, fueron determinadas a partir de ajustes empíricos de registros hidrológicos.
En la literatura existen múltiples expresiones para el cálculo del tiempo de concentración propuestas por diferentes autores: Temez, William, Kirpich, California Coulverts Practice, Giandotti, S.C.S, Ventura -Heron, Brausby-William, Passini, Izzard (1946), Federal Aviation Administration (1970), Ecuaciones de onda cinemática Morgali y Linsley (1965) Aron y Erborge (1973).
Debido a las diferentes formas como fueron concebidas estas expresiones, la variabilidad de los resultados entre una y otra puede ser bastante alta, razón por la cual el criterio del analista juega un papel fundamental en la definición del tiempo de concentración de una determinada cuenca.
Témez.
Tc: Tiempo de concentración en horas, L: Longitud del cauce principal en kilómetros, So: Diferencia de cotas sobre L en porcentaje.

Williams.
A: área de la cuenca en millas cuadradas, L: distancia en línea recta desde el sitio de interés al punto mas alto en millas, So: diferencia de cotas entre los puntos más extremos divida por L en porcentaje, d: diámetro de una cuenca circular con área A en millas.
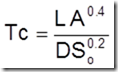
Kirpich. Desarrollada a partir de información del SCS en siete cuencas rurales de Tennessee con canales bien definidos y pendientes empinadas (3 a 10%).
L: longitud desde la estación de aforo hasta la divisoria siguiendo en cauce principal en kilómetros, So: diferencia de cotas entre los puntos extremos de la corriente en m/m.
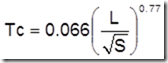
California Culverts Practice. Esencialmente es la ecuación de Kirpich; desarrollada para pequeñas cuencas montañosas en California.
L = longitud del curso de agua más largo (m), H = diferencia de nivel entre la divisoria de aguas y la salida (m).

Giandotti
tc= tiempo de concentración (horas), S= área de la cuenca (km2), L= longitud del cauce principal (km), i= elevación media de la cuenca o diferencia de nivel principal (m).

Ecuación de retardo SCS (1973).Ecuación desarrollada por el SCS a partir de información de cuencas de uso agrícola; ha sido adaptada a pequeñas cuencas urbanas con áreas inferiores a 800 Ha; se ha encontrado que generalmente es buena cuando el área se encuentra completamente pavimentada; para áreas mixtas tiene tendencia a la sobreestimación; se aplican factores de ajuste para corregir efectos de mejoras en canales e impermeabilización de superficies; la ecuación supone que tc = 1.67 x retardo de la cuenca.
L = longitud hidráulica de la cuenca mayor trayectoria de flujo (m), CN = Número de curva SCS, S = pendiente promedio de la cuenca (m/m).

Ventura-Heras
tc= tiempo de concentración (horas), i= pendiente media del cauce principal (%), S= área de la cuenca (km2), L= longitud del cauce principal (km), a= alejamiento medio

Bransby-Williams
T= tiempo de concentración (horas), L= distancia máxima a la salida (km), D= diámetro del círculo de área equivalente a la superficie de la cuenca (km2), M= área de la cuenca (km2), F= pendiente media del cauce principal (%)

Passini
tc= tiempo de concentración (horas), i= pendiente media del cauce principal (%), S= área de la cuenca (km2), L= longitud del cauce principal (km), a= alejamiento medio

Izzard
Desarrollada experimentalmente en laboratorio por el Bureau of Public Roads para flujo superficial en caminos y Áreas de céspedes; los valores del coeficiente de retardo varían desde 0.0070 para pavimentos muy lisos hasta 0.012 para pavimentos de concreto y 0.06 para superficies densamente cubiertas de pasto; la solución requiere de procesos iterativos; el producto de i por L debe ser ≤ 3800.
i = intensidad de lluvia (mm/h), c = coeficiente de retardo, L = longitud de la trayectoria de flujo (m), S = pendiente de la trayectoria de flujo (m/m).

Federal Aviation Administration
Desarrollada de información sobre el drenaje de aeropuertos recopilada por el Corps of Engineers: el método tiene como finalidad el ser usado en problemas de drenaje de aeropuertos pero ha sido frecuentemente usado para flujo superficial en cuencas urbanas.
C = coeficiente de escorrentía del método racional, L = longitud del flujo superficial (m), S = pendiente de la superficie (m/m)

Ecuaciones de onda cinemática Morgali y Linsley (1965) Aron y Erborge (1973)
Ecuación para flujo superficial desarrollada a partir de análisis de onda cinemática de la escorrentía superficial desde superficies desarrolladas; el método requiere iteraciones debido a que tanto I (Intensidad de lluvia) como Tc son desconocidos, la superposición de una curva de intensidad – duración – frecuencia da una solución gráfica directa para Tc
L = longitud del flujo superficial (m), n = coeficiente de rugosidad de Manning, I = intensidad de lluvia, mm/h, S = pendiente promedio del terreno (m/m).

Como posso calcular o tempo de concentração témez e kirpich no spatial analyst?
ResponderEliminarHola!, en el link http://www.aguaysig.com/search/label/Curso%20hidrolog%C3%ADa se explica como calcular los diferentes parametros que te ayudarán a calcular algunos tiempos de concentración
ResponderEliminarHola soy de estudiante de ingeniería civil, tu pagina me ha servido mucho a mi y a todos mis compañeros. Además de tus vídeos en Youtube.
ResponderEliminarGracias
Hola soy de estudiante de ingeniería civil, tu pagina me ha servido mucho a mi y a todos mis compañeros. Además de tus vídeos en Youtube.
ResponderEliminarGracias
Hola Daniela, me satisface mucho que compartir lo poco que se les ha servido. muchas gracias!!
Eliminarmuy buen aporte, muchas gracias
ResponderEliminarmuy buen aporte, muchas gracias
ResponderEliminarno mucho
ResponderEliminarHola, ojala en algún momento se pueda ejemplificar los diferentes métodos para una cuenca, puesto que es algo confuso determinar las diferentes longitudes y pendientes de acuerdo a cada método, con un ejemplo quedaría todo mucho mas claro... muchísimas gracias por este blog
ResponderEliminarMe parece que la formula de la FAA (Federal Aviation Agency) tiene un error, el coeficiente debe ser 3.26 no 0.7035.
ResponderEliminarSi utilizo su ecuación con valores de c=0.94, s=0.09 y L=877, el resultado es 7.43. Estoy hablando de una cuenca de 0.29 km2.
Tampoco se menciona en qué unidades está dado el resulado, suponiendo que fueran horas, es un valor muy alto para una cuena tan pequeña, y si hablamos de minutos, es un valor muy pequeño aun para esta cuenca.
Saludos.
y por cierto, esta pagina me ha sido de gran ayuda en muchas ocacioanes, muchas gracias.
Muy buena información, gracias!!!
ResponderEliminarcomo calculo tc de un jaguey
ResponderEliminarHola Pedro soy un estudiante de Geologia de la Universidad de Pamplona (Colombia), mi temática de trabajo de grado es sobre Avenidas Torrenciales, mi pregunta es cual es la ecuación mas conveniente para calcular el Tiempo de Concentración? partiendo de que estoy utilizando el CN en mis análisis
ResponderEliminarPor cierto déjeme felicitarlo por esa facilidad que tiene de difundir conocimiento de manera pedagógica.
Hola Geo95, Muchas gracias. lamentablemente no tengo esa respuesta. tu podrías sacar un promedio de todas las formulas utilizadas o tomar una muestra de aquellos tiempo similares y sacar el promedio de ellos...aquí se necesita de la experiencia que tengas
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarCordial saludo. Muchas gracias por los aportes. Tengo una duda, según las normas colombianas, el tiempo de concentración no debe superar los 20 minutos, pero no dicen qué pasa cuándo al calcular un tramo, se supera este valor. Me pueden sacar de esta duda. De nuevo muchas gracias
ResponderEliminarMuchas gracias por el aporte les agradezco infinitamente
ResponderEliminarUNA PREGUNTA AHORA QUE TIEMPO DE CONCENTRACION UTILIZAR
ResponderEliminaramigo por favor revisa la ecuación de temez, en muchas bibliográfias se cita en m/m y tu la citas en este post en %
ResponderEliminar¿Cómo relaciona el tiempo de concentración con el tiempo al pico?
ResponderEliminarQuiero que me digas que libro o qué documento especifica eso que aseguras en tu escrito: que la duración de la lluvia se asume como el tiempo de concentración.
ResponderEliminarHe revisado cientos de trabajos de hidrología y solo los que vienen hechos por ingeniero colombianos afirman esto. Pero no he leído eso en un documento o artículo.
Gracias.
El Kato